Algebra
Maths for pupils online. We provide teaching texts and problem sets.
Thursday 18 December 2014
Monday 17 December 2012
JEE free questions
1. Prove that for every prime
p,pn
does not divide
((p−1)∗n)!
.
2. Define a nice number as a rational number, with numerator and denominator positive and not exceeding some number.
N(x,y,n)
indicates the number of nice numbers, in
[0,n],a/b,a<=xandb<=y
, What is the formula for N?.
3. B.Stat question [Research problem conceived by me AFAIK]. Consider a prime number p. Consider all numbers having it as a factor. Repeatedly sum the digits of those numbers until you get a number less than or equal to p. In this sequence, will you ever get a p?2. How many numbers less than `n!` are divisible by all prime numbers less than `n`? What is the number for `1000`? Please show the work-out.
4. Prove that `2nCn` is always divisible by `2^{2}`, except when n is a power of 2.
5. Prove that `2^{n+1}C2^{n}` is divisible by 2, but not by 4, for all positive integral values of `n`.
6. Prove that, if `p` is a prime, then for any non-negative number `a`, `(a^p = a) mod p`.
7. Choose integer dimensioned rectangles (both width and height), so that, width `<= 2n` and height `<= 2n`. What is the probability that the resulting rectangle's areas is less than `n^{2}`.
a. If you were to bet on whether the resulting rectangles area will be less than `n^{2}` or not, what would you bet on?
8. Consider the quadratic equation `ax^2 + bx + c = 0`, with integer (not necessarily positive) co-efficients `a`, `b` and `c`, such that all of them are less than or equal to 100, in absolute value. How many numbers from 1 to 100 are roots of such an equation with some `a`, `b` and `c` combination?
9. Find the number for nice numbers (question 3), when numerator can exceed `x` and denominator can exceed `y`, but they should be reducible to something where they do not exceed `x` and `y`, respectively. If a formula is not possible, give an explanation why?
10. How many 4 digit numbers are there such that, the numbers are divisible by the sum of their digits?
11. How many 4 digit numbers are there such that, the numbers are divisible by the factorial of the sum of their digits?
12. How many 4 digit numbers are there such that, the minimal positive difference between their digits is 1. "minimal" means, if the number is `abcd`, then taking any combination like, `a + b + c - d` or `a - b - c + d` that results in a positive number, can one get 1? (Use only plus and minus).
13. How many 4 digit numbers are there such that, the product of the digits is not a perfect square, and not a perfect cube?
14. What is the minimum length of a string of digits, that contains all possible permutations of numbers 1 to 9?
15. Prove that such a string in 14, will be not be more than `9 * 9!` in length.
16. The distance between `2` permutations of numbers `1` to `n`, is defined as the least number of position flips, to make one permutation same as the other. For example, `123` is at a distance of `2` to `231`, because it can be got by first flipping `1` and `2` in `123`, getting `213`, then again flipping `1` and `3`, getting `231`
a. What is the minimum distance between two distinct permutations from `1` to `n`.
b. What is the maximum distance between two distinct permutations from `1` to `n`.
c. What is the sum of all pairwise distances of all permutations of `n` elements, from `1` to `n`. (Distance between `p_{a}` and `p_{b}` is counted only once, not twice).
17. In a `2m` page book, some sheets are missing. In how many ways, some `n` sheets that may be missing from the `2m` page book. (A sheet has `2` pages, no cover for the book).
18. `10000! = (100!)^{k} * p`, for some positive numbers k, p. Determine the maximum value for k.
19. Find the limit of `1/1! + 1/(1! + 2!) + 1/(1! +2! + 3!) + ...`, when the number of terms in denominator tends to infinity.
20. Prove that `1! + 2! + 3! + ... + n! < 2 * \sqrt{n} * ((n + e) / e)^n` for positive n.
21. Prove that `1! + 2! + 3! + ... + n! > (e + 1)/sqrt_{2 \pi} * (n / e)^n` for positive n.
22. Prove that `(6n + 4) C (3n + 2)` is always divisible by 3.
23. How many 10 digit numbers can be written as sum of 2 or more factorials?
24. Consider a quadrilateral to be a pythagorean, if all its sides are integers, and diagonal measures are also integers. Find all pythagorean quadrilaterals with dimensions (`<= N`).
25. Prove that `1 * 3 * 5 * 7 * .... * (4n - 1) < 2^{2n - 1} * (2n - 1)! * \sqrt{4n - 1}`. Try doing it without induction.
26. Prove that `(4n -1)! < 4^{2n-1} * ((2n -1)!)^{2} * \sqrt{4n - 1}`. No induction please.
27. Prove that there are infinitely many values of `n` for which `2nCn` is not divisible by a given odd prime number `p`.
28. Prove that `2nCn` is not divisible by a given prime number `p, iff all base `p` digits of `n` are less than `n/2`.
29. Prove that if `p` is a prime, `((p -1)! = (p - 1)) mod (p(p-1)/2)`.
30. Prove that if `p > 2` is a prime, `((p+1)^{p} = 1) mod p^{2}`.
31. Prove that if `p > 2` is a prime, `((p+1)^{p} = (p^{2} + 1)) mod p^{3}`.
32. Prove that if `p > 2` is a prime, `((p -1)! = -(p-2)! = 2(p-3)! = -6(p-4)!) mod p`.
33. Prove that if `p > 2` is a prime, `((p -1)! = (-1)^{j-1}*(p-j)!(j-1)!) mod p`.
34. Prove that if `p > 2` is a prime, `((p-2)! = 1) mod p`.
35. Prove that if `p > 2` is a prime, `((((p -1)/2)!)^{2} = (-1)^{((p+1)/2)}) mod p`.
36. The minimum length string, containing all permutation of `1, 2` and `3`, consists of 10 digits. Is it true or false?
a. In general, is it possible to achieve lower bound in question 15? Why? Why not?
37. How many 2 digit numbers are present such that, those have at most 2 factors.
38. How many 3 digit numbers are present such that, they can be written as sum of 2 squares.
39. Prove that only every 3rd number in fibonacci sequence is divisible by 2, only every 4th is divisible by 3, and every 5th by 5, and every sixth number is divisible by 8. What are the numbers for the lucas sequence? Prove them.
40. Prove that the number of prime numbers in first n fibonacci numbers, is never greater than the number of primes in the first n natural numbers.
41. Prove that, if an nth fibonacci number is a prime, then n is a prime. But the converse may not be true.
42. Prove that, if a fibonacci number is a square, there exist two other numbers such that, it is part of a pythagorean triple, along with those 2 numbers.
43. Prove that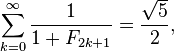
44. Prove that none of the lucas numbers are divisible by 5. Lucas series is given by Ln = ((1+sqrt(5))/2)^n + ((1-sqrt(5))/2)^n.
45. Prove also that, none of the lucas numbers are divisible by 13.
46. Prove that, if a sequence involves summing last two numbers to get the current number, it can't have all terms not divisible by 2.
47. Prove the same for 3. Prove the same for 4 also.
2. Define a nice number as a rational number, with numerator and denominator positive and not exceeding some number.
3. B.Stat question [Research problem conceived by me AFAIK]. Consider a prime number p. Consider all numbers having it as a factor. Repeatedly sum the digits of those numbers until you get a number less than or equal to p. In this sequence, will you ever get a p?2. How many numbers less than `n!` are divisible by all prime numbers less than `n`? What is the number for `1000`? Please show the work-out.
4. Prove that `2nCn` is always divisible by `2^{2}`, except when n is a power of 2.
5. Prove that `2^{n+1}C2^{n}` is divisible by 2, but not by 4, for all positive integral values of `n`.
6. Prove that, if `p` is a prime, then for any non-negative number `a`, `(a^p = a) mod p`.
7. Choose integer dimensioned rectangles (both width and height), so that, width `<= 2n` and height `<= 2n`. What is the probability that the resulting rectangle's areas is less than `n^{2}`.
a. If you were to bet on whether the resulting rectangles area will be less than `n^{2}` or not, what would you bet on?
8. Consider the quadratic equation `ax^2 + bx + c = 0`, with integer (not necessarily positive) co-efficients `a`, `b` and `c`, such that all of them are less than or equal to 100, in absolute value. How many numbers from 1 to 100 are roots of such an equation with some `a`, `b` and `c` combination?
9. Find the number for nice numbers (question 3), when numerator can exceed `x` and denominator can exceed `y`, but they should be reducible to something where they do not exceed `x` and `y`, respectively. If a formula is not possible, give an explanation why?
10. How many 4 digit numbers are there such that, the numbers are divisible by the sum of their digits?
11. How many 4 digit numbers are there such that, the numbers are divisible by the factorial of the sum of their digits?
12. How many 4 digit numbers are there such that, the minimal positive difference between their digits is 1. "minimal" means, if the number is `abcd`, then taking any combination like, `a + b + c - d` or `a - b - c + d` that results in a positive number, can one get 1? (Use only plus and minus).
13. How many 4 digit numbers are there such that, the product of the digits is not a perfect square, and not a perfect cube?
14. What is the minimum length of a string of digits, that contains all possible permutations of numbers 1 to 9?
15. Prove that such a string in 14, will be not be more than `9 * 9!` in length.
16. The distance between `2` permutations of numbers `1` to `n`, is defined as the least number of position flips, to make one permutation same as the other. For example, `123` is at a distance of `2` to `231`, because it can be got by first flipping `1` and `2` in `123`, getting `213`, then again flipping `1` and `3`, getting `231`
a. What is the minimum distance between two distinct permutations from `1` to `n`.
b. What is the maximum distance between two distinct permutations from `1` to `n`.
c. What is the sum of all pairwise distances of all permutations of `n` elements, from `1` to `n`. (Distance between `p_{a}` and `p_{b}` is counted only once, not twice).
17. In a `2m` page book, some sheets are missing. In how many ways, some `n` sheets that may be missing from the `2m` page book. (A sheet has `2` pages, no cover for the book).
18. `10000! = (100!)^{k} * p`, for some positive numbers k, p. Determine the maximum value for k.
19. Find the limit of `1/1! + 1/(1! + 2!) + 1/(1! +2! + 3!) + ...`, when the number of terms in denominator tends to infinity.
20. Prove that `1! + 2! + 3! + ... + n! < 2 * \sqrt{n} * ((n + e) / e)^n` for positive n.
21. Prove that `1! + 2! + 3! + ... + n! > (e + 1)/sqrt_{2 \pi} * (n / e)^n` for positive n.
22. Prove that `(6n + 4) C (3n + 2)` is always divisible by 3.
23. How many 10 digit numbers can be written as sum of 2 or more factorials?
24. Consider a quadrilateral to be a pythagorean, if all its sides are integers, and diagonal measures are also integers. Find all pythagorean quadrilaterals with dimensions (`<= N`).
25. Prove that `1 * 3 * 5 * 7 * .... * (4n - 1) < 2^{2n - 1} * (2n - 1)! * \sqrt{4n - 1}`. Try doing it without induction.
26. Prove that `(4n -1)! < 4^{2n-1} * ((2n -1)!)^{2} * \sqrt{4n - 1}`. No induction please.
27. Prove that there are infinitely many values of `n` for which `2nCn` is not divisible by a given odd prime number `p`.
28. Prove that `2nCn` is not divisible by a given prime number `p, iff all base `p` digits of `n` are less than `n/2`.
29. Prove that if `p` is a prime, `((p -1)! = (p - 1)) mod (p(p-1)/2)`.
30. Prove that if `p > 2` is a prime, `((p+1)^{p} = 1) mod p^{2}`.
31. Prove that if `p > 2` is a prime, `((p+1)^{p} = (p^{2} + 1)) mod p^{3}`.
32. Prove that if `p > 2` is a prime, `((p -1)! = -(p-2)! = 2(p-3)! = -6(p-4)!) mod p`.
33. Prove that if `p > 2` is a prime, `((p -1)! = (-1)^{j-1}*(p-j)!(j-1)!) mod p`.
34. Prove that if `p > 2` is a prime, `((p-2)! = 1) mod p`.
35. Prove that if `p > 2` is a prime, `((((p -1)/2)!)^{2} = (-1)^{((p+1)/2)}) mod p`.
36. The minimum length string, containing all permutation of `1, 2` and `3`, consists of 10 digits. Is it true or false?
a. In general, is it possible to achieve lower bound in question 15? Why? Why not?
37. How many 2 digit numbers are present such that, those have at most 2 factors.
38. How many 3 digit numbers are present such that, they can be written as sum of 2 squares.
39. Prove that only every 3rd number in fibonacci sequence is divisible by 2, only every 4th is divisible by 3, and every 5th by 5, and every sixth number is divisible by 8. What are the numbers for the lucas sequence? Prove them.
40. Prove that the number of prime numbers in first n fibonacci numbers, is never greater than the number of primes in the first n natural numbers.
41. Prove that, if an nth fibonacci number is a prime, then n is a prime. But the converse may not be true.
42. Prove that, if a fibonacci number is a square, there exist two other numbers such that, it is part of a pythagorean triple, along with those 2 numbers.
43. Prove that
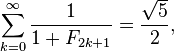
44. Prove that none of the lucas numbers are divisible by 5. Lucas series is given by Ln = ((1+sqrt(5))/2)^n + ((1-sqrt(5))/2)^n.
45. Prove also that, none of the lucas numbers are divisible by 13.
46. Prove that, if a sequence involves summing last two numbers to get the current number, it can't have all terms not divisible by 2.
47. Prove the same for 3. Prove the same for 4 also.
48. Prove that if such a sequence also does not have 5 as a factor, prove the cycle 2134 (modulo 5) occurs in such a sequence (Similar to the lucas sequence).
49. What is/are the sub-sequences in case of 13? Can there be other sequences (with different cycles), or, only similar to lucas possible there?
49. What is/are the sub-sequences in case of 13? Can there be other sequences (with different cycles), or, only similar to lucas possible there?
B Stat questions
**6. Prove that all even perfect numbers are of the form, `2^{p−1} * (2^{p}−1)` where `(2^{p}−1)` is a prime.
**7. Prove that if both `p` and `(2p + 1)` are primes, `(2p + 1)` will be a factor of `(2^{p}−1)`.
8. A triangular number (`n` th) is a number, which is got by summing the first `n`, positive integers. Prove that every number of the form `2^{p−1} * (2^{p}−1)`, is a triangular number.
9. Derive a formula for 'sum of first `n` odd cubes', and prove that every number of the form `2^{p−1} * (2^{p}−1)`, is a sum of first `n` odd cubes.
10. Even perfect numbers (except 6) give a remainder of 1, when divided with 9.
11. Subtracting 1 from a perfect number, and dividing it by 9, always gives a perfect number.
12. Summing all digits in a number, and summing all the digits in the resulting number, and repeating the process till a single digit is obtained is called, getting the "digital root" of a number. Prove that a positive number is divisible by 9, iff, its digital root is 9.
13. Any number of the form `2^{m−1} * (2^{m}−1)`, where m is any odd integer, leaves a remainder of 1 when divided with 9.
*14. An Ore's harmonic number, is a number whose factors have a harmonic mean of an integer. Prove that every perfect number is an Ore's harmonic number.
*15. Prove that, for any perfect number, sum of reciprocals of its factors is equals to two.
*16. Prove that for any integer `M`, the product of arithmetic mean of its factors and harmonic mean of the factors, is the number `M` itself.
*17. Any odd perfect number `N` is of the form, `N = q^{\alpha} * p_{1}^{2e_{1}} * p_{2}^{2e_{2}} * p_{3}^{2e_{3}} ...p_{k}^{2e_{k}}`. Where `q`, `p_{1}`, `p_{2}` are all distinct primes, with `q \equiv \alpha \equiv 1 (mod 4)`.
18. Continuing on 17, the smallest prime factor of `N` is less than `(2k + 8) / 3`.
19. Continuing on 18, prove also that `N < 2^{4^{k+1}}`.
20. Continuing on 19, prove also that the largest prime factor of `N` is greater than `10^{8}`.
21. Continuing on 20, prove also that `q^{\alpha} > 10^{62}` or `p_{j}^{2e_{j}} > 10^{62}` for some `j`.
22. Continuing on 21, prove also that the largest prime factor of `N` is greater than `10^{8}`.
23. Continuing on 22, prove also that the second largest prime factor is greater than `10^{4}`, and the third largest prime factor is greater than 100.
24. Continuing on 23, prove also that if N has at least 101 prime factors and at least 9 distinct prime factors. If 3 is not one of the factors of N, then N has at least 12 distinct prime factors.
25. Prove that an odd perfect number is not divisible by 105.
26. Every odd perfect number is of the form N ≡ 1 (mod 12), N ≡ 117 (mod 468), or N ≡ 81 (mod 324).
27. The only even perfect number of the form x3 + 1 is 28.
28. 28 is also the only even perfect number that is a sum of two positive integral cubes
29. Prove that no perfect number can be a square number.
30. The number of perfect numbers less than `n` is less than `c\sqrt{n}`, where `c > 0` is a constant.
31. Numbers where the sum is less than the number itself are called deficient, and where it is greater than the number, abundant. Give an example of each.
32. In number theory, a practical number or panarithmic number is a positive integer `n` such that all smaller positive integers can be represented as sums of distinct divisors of `n`. Prove that any even perfect number and any power of two is a practical number.
33. Prove that prime numbers are infinite. (Use proof by contradiction).
34. Prove that `2n_{C_{n}}` is divisible by a prime number n, iff, n's p-ary repesentation contains all digits less than `p / 2`.
35. Prove that if `N` is a perfect number, none of its multiples or factors is a perfect number.
36. when written in decimal notation, how many trailing zeros are present in 32!. Can you generalize it for `n`.
37. Prove that only square numbers have odd number of factors.
38. Prove that the number of factors of a number `n`, is always not greater than `2 * \lfloor\sqrt{n}\rfloor`.
39. Continuing on 38, is there any number for which the number of factors is equal to the upper bound? Why?
40. when written in decimal notation, what digit do powers of 5 end with? What about powers of 6?
41. Prove that in `x^{4} + y^{4} = z^{4}` (x, y and z are positive integers), at least one of x or y is divisible by 5.
42. Consider a number with maximum number of factors between 1 and `n^{2}`. Prove that such a number is not divisible by any prime number `p >= n`, for `n > 4`.
43. Prove that `n!` cant be a square number for any `n > 1`. (My proof involves the proven conjecture that there exists a prime number between `2n` and `3n`, for `n > 1`).
44. Every prime number `p > 3` satisfies the following: `p^{2} = 24*k + 1` for some positive number `k`.
45. Also, every prime number `p > 30` satisfies the following: `p^{4} = 240*k + 1` for some positive number `k`.
46. Prove that a composite number (`N`) definitely has a prime factor (`<= \lfloor\sqrt{n}\rfloor`).
47. Prove that the fraction of "the number of divisors of first n prime numbers", in any `N` numbers is same as `(1 - 1/2) * (1 - 1/3) * (1 - 1/5) * ...` (Denominators are all first `n` prime numbers. Hint: Generalize Eratosthenes Sieve).
48. Using `+`, `-`, `*`, `/`, `\sqrt`, `.` (decimal), `!` (factorial) and `^` (to the power of), find a way to represent 73 using four fours.
49. Do same as 48, for 77.
50. Do same as 48, for 87.
51. Do same as 48, for 93.
52. Do same as 48, for 99.
53. There is a way to represent all positive numbers using repeated trigonometric functional application on a single 4. Could you get it?
54. Prove that successive terms of a fibonacci sequence are relatively prime.
55. Prove that if the `n` th fibonacci number is denoted as `F_{n}`, `F_{n} | F_{mn}` for any m, n.
56. Consider the fibonacci sequence modulo some positive number `k`. Prove that modulo `k`, the fibonacci sequence has zeros equally spaced (periodically arranged).
57. Prove that the `n` th prime number, is less than `n^{2}`, for `n > 1`.
58. Prove that, in every 6 numbers (numbers themselves greater than 6), there can only be 2 prime numbers.
59. Continuing 58, also prove that every 15 numbers, there can only be 4 primes.
60. Continuing 59, also prove that every 35 numbers, only 8 can be primes.
61. Continuing 60, can you generalize it.
62. Continuing 61, can you generalize it as a formula representing number of prime numbers from 1 to `N`.
63. Continuing 62, we seem to sort of know when the number of primes exceeds the known prime numbers so far. So, does it give a way of finding where next prime would lie? (Well, it did not give a precise enough formula for me. Looked very promising though.)
64. Prove that the fraction of numbers relatively prime to 3 are `2/3`. Prove that the fraction of numbers relatively prime to 5 are `4/5`. Also, prove that the fraction of numbers which are relatively prime to `15` are `8/15`.
65. Continuing on 64, what do these results indicate?
66. Continuing on 65, can you generalize it (the fraction of relatively prime numbers to a number `n`) for an arbitrary number `n` (Consider the prime power expansion of `n`).
67. Show that if a number is deficient, all of its factors are deficient too.
68. Show that if a number is abundant, all of its multiples are abundant too.
69. Based on 67 and 68, devise a method to stop searching for perfect numbers, when starting search from 1 and going upwards.
70. Prove that no prime number is a perfect number.
71. Prove that no number of the form `p_{1}^{k_{1}}`, where `p_{1}` is a prime can be a perfect number.
72. Prove that no number of the form `p_{1}^{k_{1}} * p_{2}^{k_{2}}`, where `p_{1} > 2` and `p_{2} > p_{1}` are primes can be a perfect number.
73. Prove that, if all prime factors of a perfect number (`N`) are more than `p`, prove that `N` must have at least `log_{p/(p-1)}^{2}` number of prime factors.
74. Prove that, for any prime number p, `a^{(p-1)*n} + b^{(p-1)*n} = c^{(p-1)*n}` for any positive n, and positive numbers a, b and c, implies that at least one of `a`, `b` and `c` are divisible by `p`.
75. Prove that any prime factor of `(a^{5} - b^{5}) / (a - b)` is of the form of `10*k + 11`, for some non-negative k, or it is `5`.
76. Generalize 75, generalize about any prime factor of `(a^{p} - b^{p}) / (a - b)` where `p` is a prime number.
77. Continuing on 75, also prove that 5 is a factor of that expression, iff `(a - b)` is divisible by 5.
78. Generalize similarly for a generic prime exponent `p`.
79. Depending on 75-78, consider a equality of the form `a^{5} - b^{5} = c^{5} - d^{5}`. Prove that if `(a - b)` is divisible by a prime number `p` not of the form `10*k + 11`, then `(c - d)` also is divisible by `p`. (Taxicab problem related).
80. Can we say something about `a` (or `b`) in the equation, `a^{p} + b^{p} = c^{p}`. What observation can be made about it?
81. How many 2 digit numbers are divisible by the digits in them. (If same digit occurs multiple times, divide multiple times with the digit. Exclude zeroes from divisors)
82. How many three digit numbers are divisible by all digits in them
83. If `n! + 1 = m^{2}` has solutions, then `n!` (consider `n` beyond trivial ones for which we know some solution, like, 4, 5 and 7) can be factorized into two numbers `a` and `b` such that `a - b = 2`, and `ab = n!`.
84. Continuing on 83, `a` and `b` are such that, one of them is divisible by 2 but not by 4.
85. Continuing on 84, `a` and `b` are such that, every prime number `n > p > 2`, is a factor of exactly one of them, but not both.
86. Continuing on 85, `a` is of the form `2 * op_{1}^{k_{1}} * op_{2}^{k_{2}} * op_{3}^{k_{3}} * ...` and `b` is of the form `2^{k} * op_{a}^{k_{a}} * op_{b}^{k_{b}} * op_{c}^{k_{c}} * ...` where `op_{i}` are all distinct odd primes.
87. Continuing on 86, you have to prove that for large `k`, `op_{1}^{k_{1}} * op_{2}^{k_{2}} * op_{3}^{k_{3}} ... + 1` (or `-1`), where `op_{i}` are odd-primes cannot have high powers of 2 as a factor (for solving the Brocard's problem). Proof, anyone?
88. Continuing on 87, prove that `3^{n} + 1` is divisible by either 2 or 4, but not by higher powers of 2.
89. Continuing on 88, prove that `5^{n} + 1` is always divisible by 2, but not by higher powers of 2.
90. Continuing on 89, prove that `p^{2n} + 1`, where `p` is a prime number, is always divisible by 2, but not by 4.
91. Continuing on 90, prove that `p^{2n+1} + 1` is divisible by the same power of 2, that divides `p + 1`.
92. Continuing on 91, prove that `3^{2n+1} - 1` is always divisible by 2, but not by higher powers of 2.
93. Continuing on 92, prove that `5^{2n+1} - 1` is always divisible by 4, but not by higher powers of 2.
94. Continuing on 93, prove that `p^{2n + 1} - 1`, where `p` is a prime number, is always divisible by the same power of 2, that divides `p - 1`.
95. Continuing on 94, prove that `p^{2n} - 1`, where `p` is a prime number, is always divisible by same power of 2 (`r`), unless `n` is a power of 2 itself.
96. Continuing on 95, prove that `p^{2^{n}} - 1`, where `p` is a prime number, is always divisible by `2^{n+k}`, where `2^{k}` divides `p^{2i} - 1` maximally, where `i` is not of the form `2^{o}`.
97. Continuing on 96, one can give simpler formulation of problem in 83. For this, prove that `2^{n}` is never a factor of `n!`.
98. Continuing on 97, prove that `n!` always has a factor of the form `2^{(1 - \delta) * n}`, where `\delta` decreases with increasing `n`.
99. Continuing on 98 and 83, for such an `n` to exist, you have to prove that for large `n`, `op_{1}^{k_{1}} * op_{2}^{k_{2}} * op_{3}^{k_{3}} ... + 1` (or `-1`), where `op_{i}` are odd-primes should divide `2^{(7 * n)/8}` (`(7 * n) / 8` is for instance).
100. Prove that `2^{p−1} * (2^{p}−1)` is an even perfect number whenever `2^{p}−1` is a prime (Euclid).
101. Prove that, if `p` is an odd number such that `p + 1 = 2^{k_{1}}*o_{1}`, where `o_{1}` is an odd number and `k_{1} > 1`, and `q` is another similar number (like `p`), then `pq + 1` is divisible by 2 and not by 4.
102. Prove that, if `p` is an odd number such that `p + 1 = 2*o_{1}`, where `o_{1}` is an odd number, and `q` is another similar number (like `p`), then `pq + 1` is divisible by 2 and not by 4.
103. Prove that, if `p` is an odd number such that `p - 1 = 2^{k_{1}}*o_{1}`, where `o_{1}` is an odd number and `k_{1} >= 1`, and `q` is another similar number (like `p`), then `pq - 1` is divisible by `min(k_{1}, k_{2})` unless `k_{1} = k_{2}`.
104. Prove that, if `p` is an odd number such that `p + 1 = 2^{k_{1}}*o_{1}`, where `o_{1}` is an odd number, and `q` is another similar number (like `p`), then `pq + 1` is divisible by highers powers of 2 than (`2^{1}`), iff, exactly one of `k_{1}` and `k_{2}` is equal to `1`.
105. Prove that, `op_{1}^{k_{1}} * op_{2}^{k_{2}} * op_{3}^{k_{3}} * ... + 1` where `op_{i}` are odd primes, can be reduced to something that divides 2 but not 4, or, something of the form `(2*o_{1} - 1) * (2^{k}*o_{2} - 1) + 1` for some odd numbers `o_{1}` and `o_{2}`.
106. State and prove the conditions where the expression in 105 divides only 2 but not 4.
107. Consider the case in 105, where `o_{1} = 1`. In this case, prove that it does not result in an `n` such that `n! + 1 = m^{2}`. (`k` is not as big as `(7*n)/8`).
108. Continuing on 103, prove that all prime numbers between `n/i` and `n/(i+1)` (where `i >= 1`) have the same power in `n!`.
109. Continuing on 103, prove that only the prime numbers between `n/2` and `n` have an exponent of `1`, in the prime number expansion of `n`.
110. Continuing on 10, consider `(2^{k}*o_{2} - 1) = 3^{k_{1}}` (Since any such prime number would do). Prove that if `3^{k_{1}}` divides `2^{l} - 1`, then `l` is such that `l = (4 * k_{1} - 2)`.
111. Prove that, `\pi . p_{i}^(1 / (p_{i} - 1))` (Here, `\pi` means product of), where `p_{i}` are prime numbers (starting from `2`), does not converge as `i` increases.
112. Continuing on 111, prove that the lower-bound of the expression in 111, is, `(2\pi n)^{1/(2n)} . n/e` where `e` is the natural logarithm base (Hint: Remember something, yeah!).
113. Prove that, if `2n` numbers are present, where the minimum difference between then is `\delta` and maximum difference is a polynomial function of `\delta` with constant term zero, then any difference between two terms formed by multiplying `n` each numbers is always divisible by `\delta`.
114. Prove that the exponent of prime number `p` in `n!` is always not less than `(n + 1)/(p -1) * (1 - 1/(p^{\lfloor log_{p}^{n} \rfloor})) - \lfloor log_{p}^{n} \rfloor`.
115. Prove that the exponent of prime number `p` in `n!` is always not greater than `n/(p -1) * (1 - 1/(p^{\lfloor log_{p}^{n} \rfloor}))`
116. Prove that, all numbers between `n/i` and `n/(i + 1)` have same power in prime number expansion of `n!`, whenever `i < \sqrt (n)`.
117. Continuing on 116, prove that, for two prime numbers `p_{1}` and `p_{2}`, belonging to same interval (`p_{1} > p_{2}`), and having exponent `k` in prime number expansion of `n!`, the ratio of `p_{1}^{k}` to `p_{2}^{k}` is always less than `e` (the natural log base).
118. Also prove that, when a solution to Brocard's problem exists, the prime terms in expansion of `n!`, should be distributed across two terms (`A` and `B`) such that, `A - B = 1`, and `AB * 4 = n! + 1`.
119. Continuing on 118, prove that either `A` or `B` contains `2^({k_{1}} - 2)`, where `k_{1}` is the exponent of `2` in `n!` (meaning, its prime number expansion).
120. Continuing on 119, prove that if equal number of prime numbers are segregated into `A` and `B`, a solution to Brocard's problem is not possible. (Use 113).
121. Continuing on 117, if prime numbers within same interval, are factored such that equal number of them are in `A` and in `B`, then give an estimate of their ratio, in terms of `e` (Reduce the ratio as much as possible).
122. Prove that for large `n`, the smallest term, in the prime number expansion of `n!` is always not lesser than `(n + 1) / 2`.
123. MRB constant is given by , `\sigma_{n=1} (-1)^{n} * 1/(n^{n})` (till infinity). Prove that, for any first `n` terms of the MRB constant (denoted by `MRB(n)`), `(MRB(n))^{n!^{n}}` is a rational number.
124. Prove that, any sub-sequence of terms for the MRB constant, is not a transcendental number.
125. Prove that only 3 is a possible common prime factor of x + 1, and x^2 - x + 1, whenever x is an integer.
126. Prove that the same 3 is the only possible common prime factor of x - 1 and x^2 + x + 1.
127. Prove that x - 1, x + 1 and x^2 + 1 can at most have one pair-wise common prime factor, that is 2.
128. Prove that in the factorization of x^(2n+1) +/- 1, if the two factors have a common factor, that factor also divides (2n+1).
129. Prove that, for x^3 +/- 1 = y^2, (y is not 3) to happen, x +/- 1 should be divisible by 3.
130. For any n, n^2 - n + 1 could be divisible by 3, but never by 9. Prove the same for n^2 + n + 1.
131.
Saturday 15 December 2012
Algebra (Functions) questions
1. Prove that (2m+1)^2 + (2n+1)^2 = (2p)^3 has no integer solutions.
2. Prove that, if (2m+1)^2 == 1 (mod 8) holds always.
3. If f(x + y) = f(x) + f(y) for all real numbers. then f(0) = 0.
4. From q3, prove that, f(n) = nf(1) for all natural numbers n.
5. Prove 4, for all rational numbers.
6. Prove 4, for all real numbers.
7. Prove that, for function in 3, f(x)/x is always a constant. What is this constant equal to.
8. If f(x + y) = f(x) + f(y) for all real numbers, prove that f(x) - f(y) = f (x - y).
9. If f(x + y) = f(x) + f(y) for all real numbers, prove that f is an odd function.
10. If f(x + y) = f(x)f(y) for all real numbers, prove that f(0) = 1 (Do not consider trivial definition of f).
11. From q10, prove that, f(n) = [f(1)]^n for all natural numbers n.
12. Prove 11, for all rational numbers.
13. Like f(x)/x in q7, what is constant for this class of functions?
14. Consider f(xy) = f(x) + f(y) for all reals. Prove that f(1) = 0.
15. Prove that f(m^n) = nf(m) for function class defined in 14. Where n and m are natural numbers.
16. Prove 15, for positive rational numbers m and n.
17. Like f(x)/x in q7, what is constant for this class of functions?
18. Consider f(xy) = f(x)f(y) for all reals. Prove that f(0) = 0. (Do not consider trivial definitions)
19. For 18, prove that f(1) = 1. (Do not consider trivial definitions)
20. If f(p) for a prime number p is always a composite number, prove that the f in 18, does not have any prime numbers as values.
21. If f is a family of linear functions, such that, any two functions f1 and f2 from f, satisfy the condition that, f1(f2(x)) == f2(f1(x)). Derive the condition that ensures this property, for family f.
22. What is such a condition for quadratic class of functions. (Quadratic polynomial necessarily will have non-zero leading coefficient).
23. Prove that if a1^(a2^x) = a2^(a1^x) for all x real, then a1 = a2.
24. log_a1(x) = log_x(a1), then what is x?
25. Prove that a^n + b^n = 2^n has no solutions apart from trivial ones.
26. Prove that a^2 - b^2 = c^3 has infinitely many solutions.
27. (2a+1)^2 + (2b+1)^2 = (2c)^3 has no solutions.
28. x^2 - y^2 = 6 has no solutions
29. x^m - y^m = 6 has no solutions
30. [UNSOLVED] Find x, y, m and n such that x^m - y^n = 6.
31. a^2 + b^2 = 2^n implies that a = b.
32. a^2 + b^2 = 2^n implies that a and b are even
33. Prove that a^2 - b^2 = c^n has infinitely many solutions.
34. Consider a function with this property.
f(x^m +/- y^n) = x^(m-1) * f(x) +/- y^(n-1) * f(y) (both m and n are at least 2).
Prove that f(0) = 0
35. Using the function specified in 34, prove that f(1) + f(-1) = 0
36. Using the function specified in 34, prove that f(2) = 2f(1)
37. Using the function specified in 34, prove that f(5) = 5f(1)
38. Using the function specified in 34, prove that f(3) = 3f(1)
39. Using the function specified in 34, prove that f(39) = 39f(1)
40. Prove that, for every odd number f is defined.
41. Prove that, for every even number of the form 4k, the function f is defined.
42. Prove that, all even numbers of the form 24k^2 + 2 have definition of f.
43. Prove that, all even numbers of the form (5k^2 + 375)/12 (of the form (4l+2) also) have definition of f.
44. Prove that, all even numbers of the form 18(k^2 + 3) have definition of f.
45. x^2 - y^2 = 14, no solution exists
46. x^m - y^m = 14, no solution exists
47. x^2 - y^2 = 30, no solution exists
48. x^m - y^m = 30, no solution exists
49. p^2 = 16k + 5, no solution exists
50. p^2 = 16k + 3, no solution exists
51. p^2 = 16k + 7, no solution exists
52. For which remainders (when p^2 is divided by 16) do solutions exist, and why?
53. When all squares are taken modulo 16, which moduli are more frequent than others?
54. Last digit in 2^2^2^.... 1000 times?
55. Consider a function with this property.
f(x^m +/- y^n +/- z^p) = x^(m-1) * f(x) +/- y^(n-1) * f(y) +/- z^(p-1) f(z) (m, n and p are at least 2).
Prove that f(0) = 0
56. Prove that f(6) = 6f(1).
57. Prove that f(14) = 14f(1).
*58. Is there a number n for which this function could not be defined?
59. Prove that if x^m - y^n = 6, then x and y are relatively prime.
60. Prove that if x^m - y^n = 6, then m and n are relatively prime.
61. Prove that if m^m - n^n = 6, has no solutions.
62. Prove that k^p - p^k = 6 has no solutions.
63. Prove that k^k - (k/2)^2k = 6 has no solutions.
64. Prove that k^2 = 0, 1 or 4 mod 8.
65. If f(x^n) = nx^(n-1)f(x), prove that f(1) = 0
66. For function in 65, prove also that f(0) = 0
67. For function in 65, prove also that f(4) = 2f(2)
68. For function in 65, prove also that f(x^2) = 2xf(x)
69. For function in 65, prove also that f(x^4) = 2x^2f(x^2)
70. For function in 65, prove also that f(x^mn) = mx^((m-1)*n)f(x^n)
71. Which function does the one in 65 remind you of?
72.
2. Prove that, if (2m+1)^2 == 1 (mod 8) holds always.
3. If f(x + y) = f(x) + f(y) for all real numbers. then f(0) = 0.
4. From q3, prove that, f(n) = nf(1) for all natural numbers n.
5. Prove 4, for all rational numbers.
6. Prove 4, for all real numbers.
7. Prove that, for function in 3, f(x)/x is always a constant. What is this constant equal to.
8. If f(x + y) = f(x) + f(y) for all real numbers, prove that f(x) - f(y) = f (x - y).
9. If f(x + y) = f(x) + f(y) for all real numbers, prove that f is an odd function.
10. If f(x + y) = f(x)f(y) for all real numbers, prove that f(0) = 1 (Do not consider trivial definition of f).
11. From q10, prove that, f(n) = [f(1)]^n for all natural numbers n.
12. Prove 11, for all rational numbers.
13. Like f(x)/x in q7, what is constant for this class of functions?
14. Consider f(xy) = f(x) + f(y) for all reals. Prove that f(1) = 0.
15. Prove that f(m^n) = nf(m) for function class defined in 14. Where n and m are natural numbers.
16. Prove 15, for positive rational numbers m and n.
17. Like f(x)/x in q7, what is constant for this class of functions?
18. Consider f(xy) = f(x)f(y) for all reals. Prove that f(0) = 0. (Do not consider trivial definitions)
19. For 18, prove that f(1) = 1. (Do not consider trivial definitions)
20. If f(p) for a prime number p is always a composite number, prove that the f in 18, does not have any prime numbers as values.
21. If f is a family of linear functions, such that, any two functions f1 and f2 from f, satisfy the condition that, f1(f2(x)) == f2(f1(x)). Derive the condition that ensures this property, for family f.
22. What is such a condition for quadratic class of functions. (Quadratic polynomial necessarily will have non-zero leading coefficient).
23. Prove that if a1^(a2^x) = a2^(a1^x) for all x real, then a1 = a2.
24. log_a1(x) = log_x(a1), then what is x?
25. Prove that a^n + b^n = 2^n has no solutions apart from trivial ones.
26. Prove that a^2 - b^2 = c^3 has infinitely many solutions.
27. (2a+1)^2 + (2b+1)^2 = (2c)^3 has no solutions.
28. x^2 - y^2 = 6 has no solutions
29. x^m - y^m = 6 has no solutions
30. [UNSOLVED] Find x, y, m and n such that x^m - y^n = 6.
31. a^2 + b^2 = 2^n implies that a = b.
32. a^2 + b^2 = 2^n implies that a and b are even
33. Prove that a^2 - b^2 = c^n has infinitely many solutions.
34. Consider a function with this property.
f(x^m +/- y^n) = x^(m-1) * f(x) +/- y^(n-1) * f(y) (both m and n are at least 2).
Prove that f(0) = 0
35. Using the function specified in 34, prove that f(1) + f(-1) = 0
36. Using the function specified in 34, prove that f(2) = 2f(1)
37. Using the function specified in 34, prove that f(5) = 5f(1)
38. Using the function specified in 34, prove that f(3) = 3f(1)
39. Using the function specified in 34, prove that f(39) = 39f(1)
40. Prove that, for every odd number f is defined.
41. Prove that, for every even number of the form 4k, the function f is defined.
42. Prove that, all even numbers of the form 24k^2 + 2 have definition of f.
43. Prove that, all even numbers of the form (5k^2 + 375)/12 (of the form (4l+2) also) have definition of f.
44. Prove that, all even numbers of the form 18(k^2 + 3) have definition of f.
45. x^2 - y^2 = 14, no solution exists
46. x^m - y^m = 14, no solution exists
47. x^2 - y^2 = 30, no solution exists
48. x^m - y^m = 30, no solution exists
49. p^2 = 16k + 5, no solution exists
50. p^2 = 16k + 3, no solution exists
51. p^2 = 16k + 7, no solution exists
52. For which remainders (when p^2 is divided by 16) do solutions exist, and why?
53. When all squares are taken modulo 16, which moduli are more frequent than others?
54. Last digit in 2^2^2^.... 1000 times?
55. Consider a function with this property.
f(x^m +/- y^n +/- z^p) = x^(m-1) * f(x) +/- y^(n-1) * f(y) +/- z^(p-1) f(z) (m, n and p are at least 2).
Prove that f(0) = 0
56. Prove that f(6) = 6f(1).
57. Prove that f(14) = 14f(1).
*58. Is there a number n for which this function could not be defined?
59. Prove that if x^m - y^n = 6, then x and y are relatively prime.
60. Prove that if x^m - y^n = 6, then m and n are relatively prime.
61. Prove that if m^m - n^n = 6, has no solutions.
62. Prove that k^p - p^k = 6 has no solutions.
63. Prove that k^k - (k/2)^2k = 6 has no solutions.
64. Prove that k^2 = 0, 1 or 4 mod 8.
65. If f(x^n) = nx^(n-1)f(x), prove that f(1) = 0
66. For function in 65, prove also that f(0) = 0
67. For function in 65, prove also that f(4) = 2f(2)
68. For function in 65, prove also that f(x^2) = 2xf(x)
69. For function in 65, prove also that f(x^4) = 2x^2f(x^2)
70. For function in 65, prove also that f(x^mn) = mx^((m-1)*n)f(x^n)
71. Which function does the one in 65 remind you of?
72.
Friday 14 December 2012
IIT JEE Sample Maths paper 2
1. 25 people are sitting in 3 concentric circles with one person sitting
at the center. Every circle has 8 people sitting, and everyone is
sitting on radii that are spaced 45 degrees, with 4 people on every such
line. Find out number of permutations in such a scenario.
2. There is a circle, for which a maximal square is inscribed in it. After erasing two opposite sides of a square, places were marked for people to sit on the sides of square and on the circle. Circle has 16 people equi-spaced, and each side has 3 people equi-spaced (There is one person at the ends of each side, where it meets the circle). Given 22 people, how many such arrangements are possible?
3. Consider a rectangle of dimensions m * n. There are 3 possible moves, for someone at square (0, 0) in order to reach square (m, n). Upwards, which moves one from (a, b) to (a, b+1), right side which is (a, b) to (a+1, b). and diagonal, which is (a, b) to (a+1, b+1). How many possible routes are there to reach (m, n) from (0, 0).
4. Consider a move where; instead of diagonal move, one moves to (a+2, b+1) from (a, b) in two moves. Calculate the number of different routes, and minimal number of moves.
5. Generalize for the case of (a+n, b+1) from (a, b) in n moves, and minimal number of moves.
6. Generalize for the case of (a+1, b+n) from (a, b) in n moves, and minimal number of moves.
7. Generalize for the case of (a+n, b+1) from (a, b) in 1 move, and minimal number of moves.
8. Generalize for the case of (a+1, b+n) from (a, b) in 1 move, and minimal number of moves.
9. Consider the circular configuration in problem 1. From any point (point is where a person used to sit in problem 1) on the outermost circle, reaching the center can be done by moving from one point to another by
a. going inward
b. going to left
c. going to right
Calculate the number of possible routes. One is allowed to visit a point, at-most once only.
10. Generalize for n points around the circle's circumference.
11. Generalize for n concentric circles.
12. Generalize for both as in problems 10 and 11
13. Do problem 9, without "move b".
14. Consider a circular sector of angle 90 degrees. Consider n such concentric sectors. The various sectors are joined by straight lines (radii) at angle 0, 10, 20, ... 90 degrees. Considering points at every intersection, and using moves a,b and c from 9, find how many possible paths exist to reach the center from any point on the outermost sector.
15. A hop is similar to diagonal move, in sense that, it is used to jump when there can be a diagonal between points. Include left side inward hop as a possible move, and solve 9.
16. Include hop move and solve problem 14.
17. Include hops like what is presented in problems 5-8 and solve 9.
18. Include hops like what is presented in problems 5-8 and solve 14.
19. Consider natural numbers in a line, starting from zero. 2 pieces move along the line as follows, both starting from zero.
i. Roll a dice, and move accordingly, so many points, from 1 to 6.
Find out the number of possible locations (as ordered pairs, first piece followed by the second) after n moves.
20. Consider the following change to 19.
i. If piece 1 plays dice and lands up in the same square as piece 2, it will be reset, meaning sent back to 0 on the line. (Similarly for piece 2).
Now find the number of possible locations, after say 100 moves.
21. What is the expected position of piece (any piece) from question 19, after n moves.
22. What is the expected position of piece from question 20, after n moves.
23. Consider the following:
i. If a roll of dice results in a 6, the piece is allowed another roll. It finally moves the sum of rolled dice, as in, first comes 6. Next comes 5 in the rolls. Then it moves 6 + 5 = 11 points on the line.
Now, find the number of possible locations.
24. Use 23, and repeat with condition of question 20
25. Use 23, and find the expected position of a piece (Use conditions from q19).
26. Use 23, and find the expected position of a piece (Use conditions from q20).
27. What is the expected distance between the pieces, from q19. (There is no negative distance, all distances are positive).
28. Repeat 27, for q20 conditions
29. Repeat 27, for q23 conditions
30. Find the expected location of a piece, after the first move, under following conditions on top of q19 conditions.
i. If a roll results in a 6, the dice are allowed to be rolled again. If it gets another 6, it is rolled once again and so on and so forth.
2. There is a circle, for which a maximal square is inscribed in it. After erasing two opposite sides of a square, places were marked for people to sit on the sides of square and on the circle. Circle has 16 people equi-spaced, and each side has 3 people equi-spaced (There is one person at the ends of each side, where it meets the circle). Given 22 people, how many such arrangements are possible?
3. Consider a rectangle of dimensions m * n. There are 3 possible moves, for someone at square (0, 0) in order to reach square (m, n). Upwards, which moves one from (a, b) to (a, b+1), right side which is (a, b) to (a+1, b). and diagonal, which is (a, b) to (a+1, b+1). How many possible routes are there to reach (m, n) from (0, 0).
4. Consider a move where; instead of diagonal move, one moves to (a+2, b+1) from (a, b) in two moves. Calculate the number of different routes, and minimal number of moves.
5. Generalize for the case of (a+n, b+1) from (a, b) in n moves, and minimal number of moves.
6. Generalize for the case of (a+1, b+n) from (a, b) in n moves, and minimal number of moves.
7. Generalize for the case of (a+n, b+1) from (a, b) in 1 move, and minimal number of moves.
8. Generalize for the case of (a+1, b+n) from (a, b) in 1 move, and minimal number of moves.
9. Consider the circular configuration in problem 1. From any point (point is where a person used to sit in problem 1) on the outermost circle, reaching the center can be done by moving from one point to another by
a. going inward
b. going to left
c. going to right
Calculate the number of possible routes. One is allowed to visit a point, at-most once only.
10. Generalize for n points around the circle's circumference.
11. Generalize for n concentric circles.
12. Generalize for both as in problems 10 and 11
13. Do problem 9, without "move b".
14. Consider a circular sector of angle 90 degrees. Consider n such concentric sectors. The various sectors are joined by straight lines (radii) at angle 0, 10, 20, ... 90 degrees. Considering points at every intersection, and using moves a,b and c from 9, find how many possible paths exist to reach the center from any point on the outermost sector.
15. A hop is similar to diagonal move, in sense that, it is used to jump when there can be a diagonal between points. Include left side inward hop as a possible move, and solve 9.
16. Include hop move and solve problem 14.
17. Include hops like what is presented in problems 5-8 and solve 9.
18. Include hops like what is presented in problems 5-8 and solve 14.
19. Consider natural numbers in a line, starting from zero. 2 pieces move along the line as follows, both starting from zero.
i. Roll a dice, and move accordingly, so many points, from 1 to 6.
Find out the number of possible locations (as ordered pairs, first piece followed by the second) after n moves.
20. Consider the following change to 19.
i. If piece 1 plays dice and lands up in the same square as piece 2, it will be reset, meaning sent back to 0 on the line. (Similarly for piece 2).
Now find the number of possible locations, after say 100 moves.
21. What is the expected position of piece (any piece) from question 19, after n moves.
22. What is the expected position of piece from question 20, after n moves.
23. Consider the following:
i. If a roll of dice results in a 6, the piece is allowed another roll. It finally moves the sum of rolled dice, as in, first comes 6. Next comes 5 in the rolls. Then it moves 6 + 5 = 11 points on the line.
Now, find the number of possible locations.
24. Use 23, and repeat with condition of question 20
25. Use 23, and find the expected position of a piece (Use conditions from q19).
26. Use 23, and find the expected position of a piece (Use conditions from q20).
27. What is the expected distance between the pieces, from q19. (There is no negative distance, all distances are positive).
28. Repeat 27, for q20 conditions
29. Repeat 27, for q23 conditions
30. Find the expected location of a piece, after the first move, under following conditions on top of q19 conditions.
i. If a roll results in a 6, the dice are allowed to be rolled again. If it gets another 6, it is rolled once again and so on and so forth.
Wednesday 7 November 2012
JEE maths sample paper
Permutations and Combinations.
1. How many numbers less than `n!` are divisible by all prime numbers less than `n`? What is the number for `1000`? Please show the work-out.
2. Prove that `2nCn` is always divisible by `2^{2}`, except when n is a power of 2.
3. Prove that `2^{n+1}C2^{n}` is divisible by 2, but not by 4, for all positive integral values of `n`.
4. Prove that, if `p` is a prime, then for any non-negative number `a`, `(a^p = a) mod p`.
5. Choose integer dimensioned rectangles (both width and height), so that, width `<= 2n` and height `<= 2n`. What is the probability that the resulting rectangle's areas is less than `n^{2}`.
a. If you were to bet on whether the resulting rectangles area will be less than `n^{2}` or not, what would you bet on?
6. Consider the quadratic equation `ax^2 + bx + c = 0`, with integer (not necessarily positive) co-efficients `a`, `b` and `c`, such that all of them are less than or equal to 100, in absolute value. How many numbers from 1 to 100 are roots of such an equation with some `a`, `b` and `c` combination?
7. Define a nice number as a rational number, with numerator and denominator positive and not exceeding some number. indicates the number of nice numbers, in , What is the formula for N?.
8. Find the number for nice numbers (question 3), when numerator can exceed `x` and denominator can exceed `y`, but they should be reducible to something where they do not exceed `x` and `y`, respectively. If a formula is not possible, give an explanation why?
9. How many 4 digit numbers are there such that, the minimal positive difference between their digits is 1. "minimal" means, if the number is `abcd`, then taking any combination like, `a + b + c - d` or `a - b - c + d` that results in a positive number, can one get 1? (Use only plus and minus).
10. What is the minimum length (lower bound) of a string of digits, that contains all possible permutations of numbers 1 to 9?
a. Prove that such a string will be not be more than `9 * 9!` in length.
a. Prove that such a string will be not be more than `9 * 9!` in length.
11. The distance between `2` permutations of numbers `1` to `n`, is
defined as the least number of position flips, to make one permutation
same as the other. For example, `123` is at a distance of `2` to `231`,
because it can be got by first flipping `1` and `2` in `123`, getting
`213`, then again flipping `1` and `3`, getting `231`
a. What is the minimum distance between two distinct permutations from `1` to `n`.
b. What is the maximum distance between two distinct permutations from `1` to `n`.
c. What is the sum of all pairwise distances of all permutations of `n` elements, from `1` to `n`. (Distance between `p_{a}` and `p_{b}` is counted only once, not twice).
a. What is the minimum distance between two distinct permutations from `1` to `n`.
b. What is the maximum distance between two distinct permutations from `1` to `n`.
c. What is the sum of all pairwise distances of all permutations of `n` elements, from `1` to `n`. (Distance between `p_{a}` and `p_{b}` is counted only once, not twice).
12. In a `2m` page book, some sheets are missing. In how many ways, some
`n` sheets that may be missing from the `2m` page book. (A sheet has
`2` pages, no cover for the book).
13. `10000! = (100!)^{k} * p`, for some positive numbers k, p. Determine the maximum value for k.
14. Find the limit of `1/1! + 1/(1! + 2!) + 1/(1! +2! + 3!) + ...`, when the number of terms in denominator tends to infinity.
13. `10000! = (100!)^{k} * p`, for some positive numbers k, p. Determine the maximum value for k.
14. Find the limit of `1/1! + 1/(1! + 2!) + 1/(1! +2! + 3!) + ...`, when the number of terms in denominator tends to infinity.
15. Prove that `1! + 2! + 3! + ... + n! < 2 * \sqrt{n} * ((n + e) / e)^n` for positive n.
16. Prove that `1! + 2! + 3! + ... + n! > (e + 1)/sqrt_{2 \pi} * (n / e)^n` for positive n.
17. Prove that `(6n + 4) C (3n + 2)` is always divisible by 3.
16. Prove that `1! + 2! + 3! + ... + n! > (e + 1)/sqrt_{2 \pi} * (n / e)^n` for positive n.
17. Prove that `(6n + 4) C (3n + 2)` is always divisible by 3.
18. Consider a quadrilateral to be a pythagorean, if all its sides are
integers, and diagonal measures are also integers. Find the number of
pythagorean quadrilaterals with dimensions (`<= N`).
19. Prove that there are infinitely many values of `n` for which `2nCn` is not divisible by a given odd prime number `p`.
20. Prove that only every 3rd number in fibonacci sequence is divisible
by 2, only every 4th is divisible by 3, and every 5th by 5, and every
sixth number is divisible by 8. What are the numbers for the lucas
sequence? Prove them.
(Many more sample papers available on purchase).
Monday 5 November 2012
Calculus: The concepts of limit and infinity
"Limit n tends to infinity", something that people use often in
calculus. And this is what baffles some students as these concepts are
unknown to them till the study of calculus starts. It can be said that
the other notions of calculus, like continuity and differentiability
etc... depend on these concepts, either directly or indirectly. So, it
is very important to know and understand these concepts. Here, in this
post, I will give a practical perspective on these concepts.
Long ago, someone posed this game: Take Achilles, the greatest of the warriors in Rome, and a Tortoise. Have a race between them. Say who wins? Achilles, right. But someone said otherwise. His argument is as follows:
Let tortoise start a foot ahead of Achilles. Now, start the race, with Achilles slightly behind the tortoise. Now, it takes some time for Achilles to cover the distance of 1 foot and come at par with Tortoise's starting point. Lets say, Achilles takes 1 second to cover 1 feet. But, by then, tortoise would have moved ahead, say to 1/2 foot. Again Achilles needs to cover that 1/2 foot. By the time he covers, tortoise moves ahead again, this time by somewhat smaller amount, like 1/4 foot. Achilles again has to cover that 1/4 foot. So, he reasoned that, whatever Achilles does, the tortoise will still be ahead of him (by a very small margin), and he still needs to cover that distance again. Therefore, Achilles should be losing to the Tortoise, he concluded.
But, we know, in practice that, if a better runner is behind someone in the race, he can overtake them in time. His argument says that it is impossible, but we know in practice that, it is not true. So, what is wrong with this argument (apart from being a joke on Achilles)?
A sum of infinite numbers is not always infinity
Lets consider the distances traveled by the tortoise, when Achilles was trying to reach it's current location. More clearly, tortoise moves ahead while Achilles comes to its current position, right? Lets see, how much does it move ahead.
Ok, we know that Achilles speed is 1 foot per second, and lets say tortoise's speed is 1/2 foot per second. And the tortoise is ahead by a foot, at the beginning of the race, as we said above. Achilles takes 1 second to cover the foot, by which the tortoise is ahead of him. In that 1 second time, the tortoise moves by 1 second * 1/2 foot per second = 1/2 foot distance forward.
Now (After one second), the gap between Achilles and the tortoise is 1/2 foot. Achilles needs to cover this distance. As we know his speed, he takes 1/2 second to cover it. 1/2 second = 1/2 foot / (1 foot per sec). In the same time, tortoise would have moved 1/2 second * 1/2 foot per second = 1/2 * 1/2 foot = 1/4 foot.
Next time, when Achilles gets to the tortoise's last position, it moves ahead by 1/8 foot, as you can verify. (Don't worry if you can't understand this, there is another nicer example ahead).
So, the total distance moved by the tortoise, before Achilles overtakes it, is given by, the sum of these numbers 1/2, 1/4, 1/8 etc... Now, consider the sum of first 2 terms, it is 1/2 + 1/4 = 3/4 < 1. Now, consider the sum of first three terms 1/2 + 1/4 + 1/8 = 7/8 < 1. First four would give 15/16 < 1. A pattern emerges from these sums, no matter how many of the starting terms you take, you will always get the sum to be less than 1! Isn't that surprising?
Now, consider the time taken by Achilles to travel these distances. Initially there is a gap of 1 foot between him and the tortoise, he takes 1 second (= 1 foot / 1 foot per second) to cover it. Then, it is 1/2 foot (from above), it takes 1/2 second (= 1/2 foot / 1 foot per second) for him to cover it. The times would be like, 1 second, 1/2 second, 1/4 sec, 1/8 sec etc... So, the total time for which he is trailing to the tortoise is the sum of these times, for which he is trying to catch up with it.
Consider the sum of first 2 terms, which is 1 + 1/2 = 3/2 < 2. The first three terms yield, 1 + 1/2 + 1/4 = 7/4 < 2. First four terms give, 15/8 < 2. A pattern emerges here too, no matter how many of the starting terms you take, you will always get the sum to be less than 2. So, how many ever times he was behind the tortoise, those times; all of them, happened within the first two seconds.
But...
I know what you are thinking. "But, aren't there too many such events, when Achilles is behind the tortoise. So, you mean "infinite" events can happen in a second? How is it even rational?", I can understand what you are saying. This is a perfect example, where theory follows practice.
Often, people do not understand that the theory is in fact, one possible explanation of practice, and try to reason as if the theory is of utmost importance. Any theory, is modeled after practice, takes some concepts from it, and leaves the rest away. The taken concepts form the theory. People miss this simple fact, and go on long ways to justify theories as stand-alone entities themselves.
"And, what kind of an explanation of practice is theory?", one might ask. To which the theoreticians would reply "any kind". "Any kind"!, that is true. Theory is "any kind" of explanation to reality, it does not need to be a practical explanation to practice, a physical explanation to physics, a logical explanation to logic etc... Theory can be "any kind". Exactly here, the concept of infinity comes into picture.
Strictly speaking, we do not know whether an infinite number of events can or can't happen in a second. We simply don't know. But, by assuming that is possible, we can explain the paradox above, that Achilles loses to a tortoise. Since an explanation warrants such an assumption, we assume in theory that, "infinite number of events can happen in a finite interval". This is an example, of theory following practice.
So, according to math, do infinities occur in nature? Yes, they do. They occur every second, when cars overtake other cars on road, when athletes in Olympics overtake each other, and when Earth rotates around itself. They occur always, around us, everywhere.
A common mis-conception about infinity is that, people use it just like a number. What is tan(90^0)? One would say, it is infinity. As though, infinity can be the value of something. But, this is not right. Maths could assume infinities happen always, but, the properties of infinity mandate that, it be not treated as a number. A reasonable thing to think of infinity would be "something greater than any positive number". There is no number called "infinity" anywhere.
Properties of infinity
(To be continued...)
Long ago, someone posed this game: Take Achilles, the greatest of the warriors in Rome, and a Tortoise. Have a race between them. Say who wins? Achilles, right. But someone said otherwise. His argument is as follows:
Let tortoise start a foot ahead of Achilles. Now, start the race, with Achilles slightly behind the tortoise. Now, it takes some time for Achilles to cover the distance of 1 foot and come at par with Tortoise's starting point. Lets say, Achilles takes 1 second to cover 1 feet. But, by then, tortoise would have moved ahead, say to 1/2 foot. Again Achilles needs to cover that 1/2 foot. By the time he covers, tortoise moves ahead again, this time by somewhat smaller amount, like 1/4 foot. Achilles again has to cover that 1/4 foot. So, he reasoned that, whatever Achilles does, the tortoise will still be ahead of him (by a very small margin), and he still needs to cover that distance again. Therefore, Achilles should be losing to the Tortoise, he concluded.
But, we know, in practice that, if a better runner is behind someone in the race, he can overtake them in time. His argument says that it is impossible, but we know in practice that, it is not true. So, what is wrong with this argument (apart from being a joke on Achilles)?
A sum of infinite numbers is not always infinity
Lets consider the distances traveled by the tortoise, when Achilles was trying to reach it's current location. More clearly, tortoise moves ahead while Achilles comes to its current position, right? Lets see, how much does it move ahead.
Ok, we know that Achilles speed is 1 foot per second, and lets say tortoise's speed is 1/2 foot per second. And the tortoise is ahead by a foot, at the beginning of the race, as we said above. Achilles takes 1 second to cover the foot, by which the tortoise is ahead of him. In that 1 second time, the tortoise moves by 1 second * 1/2 foot per second = 1/2 foot distance forward.
Now (After one second), the gap between Achilles and the tortoise is 1/2 foot. Achilles needs to cover this distance. As we know his speed, he takes 1/2 second to cover it. 1/2 second = 1/2 foot / (1 foot per sec). In the same time, tortoise would have moved 1/2 second * 1/2 foot per second = 1/2 * 1/2 foot = 1/4 foot.
Next time, when Achilles gets to the tortoise's last position, it moves ahead by 1/8 foot, as you can verify. (Don't worry if you can't understand this, there is another nicer example ahead).
So, the total distance moved by the tortoise, before Achilles overtakes it, is given by, the sum of these numbers 1/2, 1/4, 1/8 etc... Now, consider the sum of first 2 terms, it is 1/2 + 1/4 = 3/4 < 1. Now, consider the sum of first three terms 1/2 + 1/4 + 1/8 = 7/8 < 1. First four would give 15/16 < 1. A pattern emerges from these sums, no matter how many of the starting terms you take, you will always get the sum to be less than 1! Isn't that surprising?
Now, consider the time taken by Achilles to travel these distances. Initially there is a gap of 1 foot between him and the tortoise, he takes 1 second (= 1 foot / 1 foot per second) to cover it. Then, it is 1/2 foot (from above), it takes 1/2 second (= 1/2 foot / 1 foot per second) for him to cover it. The times would be like, 1 second, 1/2 second, 1/4 sec, 1/8 sec etc... So, the total time for which he is trailing to the tortoise is the sum of these times, for which he is trying to catch up with it.
Consider the sum of first 2 terms, which is 1 + 1/2 = 3/2 < 2. The first three terms yield, 1 + 1/2 + 1/4 = 7/4 < 2. First four terms give, 15/8 < 2. A pattern emerges here too, no matter how many of the starting terms you take, you will always get the sum to be less than 2. So, how many ever times he was behind the tortoise, those times; all of them, happened within the first two seconds.
But...
I know what you are thinking. "But, aren't there too many such events, when Achilles is behind the tortoise. So, you mean "infinite" events can happen in a second? How is it even rational?", I can understand what you are saying. This is a perfect example, where theory follows practice.
Often, people do not understand that the theory is in fact, one possible explanation of practice, and try to reason as if the theory is of utmost importance. Any theory, is modeled after practice, takes some concepts from it, and leaves the rest away. The taken concepts form the theory. People miss this simple fact, and go on long ways to justify theories as stand-alone entities themselves.
"And, what kind of an explanation of practice is theory?", one might ask. To which the theoreticians would reply "any kind". "Any kind"!, that is true. Theory is "any kind" of explanation to reality, it does not need to be a practical explanation to practice, a physical explanation to physics, a logical explanation to logic etc... Theory can be "any kind". Exactly here, the concept of infinity comes into picture.
Strictly speaking, we do not know whether an infinite number of events can or can't happen in a second. We simply don't know. But, by assuming that is possible, we can explain the paradox above, that Achilles loses to a tortoise. Since an explanation warrants such an assumption, we assume in theory that, "infinite number of events can happen in a finite interval". This is an example, of theory following practice.
So, according to math, do infinities occur in nature? Yes, they do. They occur every second, when cars overtake other cars on road, when athletes in Olympics overtake each other, and when Earth rotates around itself. They occur always, around us, everywhere.
A common mis-conception about infinity is that, people use it just like a number. What is tan(90^0)? One would say, it is infinity. As though, infinity can be the value of something. But, this is not right. Maths could assume infinities happen always, but, the properties of infinity mandate that, it be not treated as a number. A reasonable thing to think of infinity would be "something greater than any positive number". There is no number called "infinity" anywhere.
Properties of infinity
(To be continued...)
Subscribe to:
Posts (Atom)